It is possible to stack several interferograms of the same site to increase their clarity or reduce the number of fringes, thus creating an integer interferogram combination (IIC) [R13]. The combined interferogram can have a better altitude of ambiguity h_a than any of the source interferograms.

After correction for topographic and orbital contributions, the interferogram contains three kinds of information:

The number of fringes ν representing noise due to thermal noise or to partial incoherence
The number of fringes ε/h_a due to the errors ε in the DEM, where h_a is the altitude of ambiguity
The number of fringes μ caused by any differential effects, including local variations in the atmospheric thickness, as well as local ground motion between the acquisition times.

The interferogram in which the effects of topography and the 'orbital fringes' have been retrieved gives us the fractional part of:

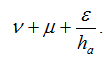
If we multiply the interferogram by an integer q₁, we will likewise multiply the number of phase transitions and the initial integer values. Note that the integer values remain unknown unless unwrapping has been performed. We obtain the fractional part of:

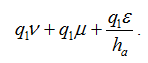
If we combine the first interferogram with a second, characterised by another independent noise distribution, another altitude of ambiguity, other differential effects and another multiplication factor q₂, but the same local DEM error ε , we obtain the fractional part of:

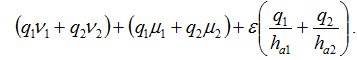
As a consequence of the multiplications, the RMS amplitude of the noise becomes:

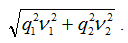
This resulting increase of the noise in practice limits the choice of the absolute value of q₁ or q₂ to less than 3.

The interferogram resulting from this kind of combination exhibits an equivalent altitude of ambiguity h_ae, written as:

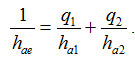
Phase unwrapping applies to altitudes of ambiguity lower than 100–200 m and greater than 10 m in interferometric conditions. Even choosing q₁ and q₂ to be �1, �2, or �3 allows us to reach an equivalent altitude of ambiguity of more than 100 m most of the time. Using this method, we create more interferometric combinations with a high altitude of ambiguity, as if we had a small orbital separation.