Polarimetric Speckle Filter

Polarimetric Speckle Filter Operator

SAR images have inherent salt and pepper like texturing called ‘speckle’ which degrades the quality of the image and makes interpretation of features more difficult. The presence of speckle intensity fluctuations in single-look complex SAR imagery is an inevitable consequence of the nature of coherent image formation. Each radar resolution cell contains multiple individual scatters, each of which contributes to the overall signal returned from the resolution cell. Since the radar wavelength is normally much smaller than the size of the resolution cell, the phase obtained from each individual scatterer is effectively random. The signals from each scatter may be summed according to the principle of superposition, which results in constructive and destructive interference. Cells where destructive interference dominates will appear to have a low reflectivity, while cells where constructive interference dominates will appear to have a high reflectivity. This leads to the phenomenon of speckle. It may be shown thatthe speckle intensity is exponentiallydistributed.

While the presence of speckle in a SAR image can impair qualitative interpretation of the image, speckle is even more problematic when interpreting SAR data in a quantitative manner. In particular, the reliability of image segmentation techniques is adversely-effected by the presence of speckle.

For polarimetric SAR data, the speckle filtering is based on incoherent averaging and requires handling statistical second order representations. Thus the speckle filtering is applied to covariance or coherency matrix.

This operator provides the following polarimetric speckle filterings:

Box Car Filter

The box car filter is a direct application of the incoherent averaging of the covariance/coherency matrix over pixels in a neighborhood defined by a sliding window. The boxcar filter presents the best filtering performance over homogeneous areas. However there are two major drawbacks with the box car filter:

    The refined Lee filter introduced below does not have these limitations.

Refined Lee Filter

The refine Lee filter in [1] is a minimum mean square error (MMSE) filter and was developed based on the multiplicative noise model. One major deficiency with the MMSE filter is that speckle noise near strong edges is not adequately filtered. To compensate this problem,  the refined Lee filter uses a nonsquare window to match the direction of edges. The filter operated in a 7x7 (or 9x9, 11x11) sliding window. One of eight edge-aligned windows is selected to filter the center pixel. Only the pixels in the non-edge area in the edge-aligned window are used in the filtering computation.

The filter follows three major processing steps as given below:

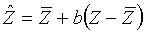
       where

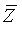
is the local mean of matrices computed with pixels in the same edge-directed window.

IDAN Filter

Conventional filtering method selects pixels from homogeneous areas in a fixed size sliding window.  The drawback with this approach is that the number of pixels selected may not be sufficient to reduce the estimation variance.  Instead of limiting  the pixel selection in a fixed size window, the IDAN (Intensity-Driven Adaptive-Neighborhood) filter proposed in [2] selects pixels with region growing techniques and criteria of the Lee sigma filter. In this algorithm, an adaptive neighborhood is determined for each pixel by a region growing technique. The pixel is then filtered with the MMSE filter computed using all selected pixels. The region growing technique consists of two stages:

Improved Lee Sigma Filter

The Lee Sigma filter proposed in [4] assumes Gaussian noise distribution and filters the center pixel in a sliding window with the average of pixels within the two-sigma range. One major drawback of the algorithm is that the mean of pixels within the two-sigma range is always underestimated due to the fact that the noise distributions are not symmetric and the symmetric thresholds are used in the pixel selection. The new Lee Sigma filter [3] extends and improves the Lee Sigma filter in the following aspects:

Input and Output

Parameters Used

   For box car filter, the following processing parameters are used by the operator (see Figure 1):



              Figure 1. Dialog box for Box Car Speckle Filter


For refined Lee filter, the following parameters are needed (see Figure 2):


                 Figure 2. Dialog box for Refined Lee Speckle Filter


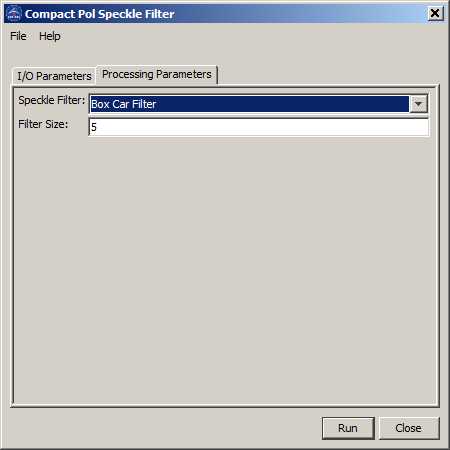
For refined Lee filter, the following parameters are needed (see Figure 3):


                 Figure 3. Dialog box for IDAN Speckle Filter


For Lee Sigma filter, the following parameters are needed (see Figure 4):



                 Figure 4. Dialog box for Improved Lee Sigma Speckle Filter


Reference: 

[1] Jong-Sen Lee and Eric Pottier, Polarimetric Radar Imaging: From Basics to Applications, CRC Press, 2009

[2] G. Vasile, E. Trouve, J.S. Lee and V. Buzuloiu, "Intensity-Driven Adaptive-Neighborhood Technique for Polarimetric and Interferometric SAR Parameters Estimation", IEEE Transaction on Geoscience and Remote Sensing, Vol. 44, No. 6, June 2006.

[3] J.S. Lee, J.H. Wen, T.L. Ainsworth, K.S. Chen and A.J. Chen, "Improved Sigma Filter for Speckle Filtering of SAR Imagery", IEEE TRansaction on Geoscience and Remote Sensing, Vol. 47, No. 1, Jan. 2009.

[4] J.S. Lee, “Digital image smoothing and the sigma filter,” Comput. Vis. Graph. Image Process., vol. 24, no. 2, pp. 255–269, Nov. 1983.