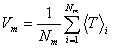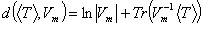Polarimetric Classification Operator

This operator performs the following polarimetric classification for a full polarimetric SAR product:

Unsupervised Cloude-Pottier Classification
Unsupervised Whishart Classification

Cloude-Pottier Classification

The Cloude-Pottier classification is an unsupervised classification scheme which is based on the use of the Entropy (H) / Alpha ( α ) plane. Entropy by definition is a natural measure of the inherent reversibility of the scattering data while alpha can be used to identify the underlying average scattering mechanisms. The H / Alpha plane is divided into nine zones corresponding to nine classes of different scattering mechanisms. For each pixel in the source product, its entropy and alpha angle are computed. Based on the position of the computed entropy and alpha in the H / Alpha plane, the pixel is classified into one of the nine zones, a zone index is assigned to the pixel. For detail calculations of entropy and alpha, readers are referred to on-line help for Polarimetric Decomposition operator. Figure 1 shows the locations and boundaries of the nine zones in H / Alpha plane:

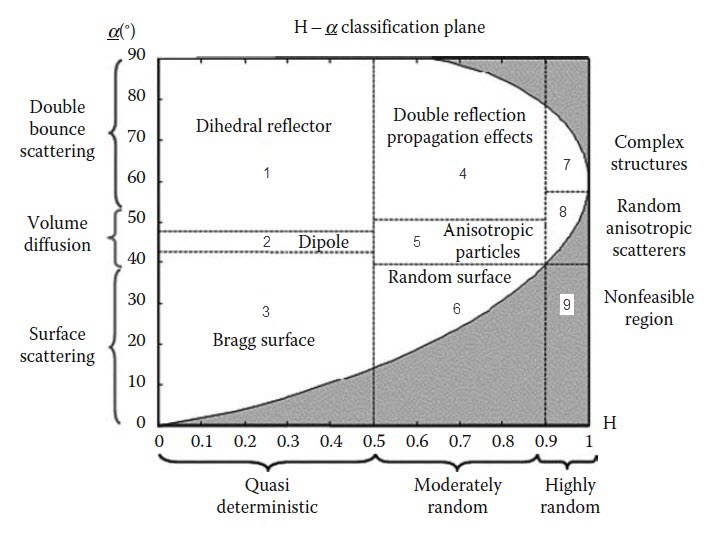
Figure 1. H / Alpha plane

H Alpha Wishart Classification

Similar to the Cloude-Pottier classification, the unsupervised H Alpha Wishart classification also separates data into nine clusters using the zones defined in the H / Alpha plane above. Different from the Cloude-Pottier classification, the H Alpha Wishart classification will continue to compute the centres of the nine clusters, then reclassify the pixels based on their Wishart distances to the cluster centres. This procedure will repeat several times until the user defined total number of iterations is reached. To achieve accurate classification result, speckle filtering must be applied before the classification.

The cluster centre V_m for the m th cluster is the average of the coherency matrices of all pixels in the cluster. Mathematically it is given by

The Wishart distance measure from coherency matrix T to cluster centre V_m is defined as the following:

where ln() is the natural logarithm function, |.| and Tr(.) indicate the determinant and the trace of the matrix respectively.

Freeman-Durden Wishart Classification

The Freeman-Durden classification is also a Wishart distance based classification. It basically implements the unsupervised PolSAR classification algorithm proposed by Lee et al. in [2]. In the algorithm, the pixels are first divided into three categories of surface, volume and double bounce scattering by applying the Freeman-Durden decomposition. Then 30 clusters are created in each category with approximately equal number of pixels based on the backscattering power of surface, volume and double bounce. Finally the clusters in each category are merged to a pre-selected number of classes based on Wishart distance between clusters.

General Wishart Classification

The General Wishart classification method generalizes the Freeman-Durden Wishart classification method above. In the General Wishart classification, the initial decomposition method is generalized from Freeman-Durden method to other decomposition method, such as Sinclair decomposition, Yamaguchi decomposition etc. The rest of the algorithm is the same as the Freeman-Durden classification algorithm.

Input and Output

The input to this operator can be covariance matrix or coherency matrix generated by Polarimetric Matrix Generation operator.
The output of this operator is a band with pixel values being the cluster indices.

Parameters Used

For Cloude-Pottier classification, the following processing parameter are needed (see Figure 2):

Classification: the classification method
Window Size: dimension of sliding window for computing mean covariance or coherency matrix

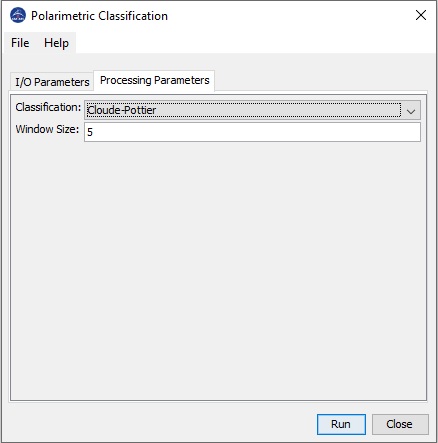
Figure 2. Dialog box for Cloude-Pottier classification

For H Alpha Wishart classification, the following parameters are used (see Figure 3):

Classification: the classification method
Window Size: dimension of sliding window for computing mean covariance or coherency matrix
Maximum Number of Iterations: the maximum number of iterations

Figure 3. Dialog box for H Alpha Wishart classification

For the Freeman-Durden Wishart classification, the following parameters are used (see Figure 4):

Classification: the classification method
Window Size: dimension of sliding window for computing mean covariance or coherency matrix
Initial Number of Classes: the initial number of clusters
Final Number of Classes: the final number of classes after classification
Threshold for Mixed Category: the threshold used in classifying pixels to the mixed category. The Freeman-Durden decomposition computes for each pixel the contribution of three scattering mechanisms: volume, surface and double-bounce. Based on the dominant value of the three categories, the pixel is classified to one of the categories. But for some pixels, there is no obvious dominant value, in this case the pixel is classified to the mixed category. Say the pixel has values Pv, Ps and Pd for the three categories, if max(Pv, Ps, Pd) / (Pv + Ps + Pd) <= this threshold, it is classified to the mixed category.

Figure 4. Dialog box for the Freeman-Durden Wishart classification

For the General Wishart classification, the following parameters are used (see Figure 4):

Classification: the classification method
Window Size: dimension of sliding window for computing mean covariance or coherency matrixp
Initial Number of Classes: the initial number of clusters
Final Number of Classes: the final number of classes after classification
Threshold for Mixed Category: the threshold used in classifying pixels to the mixed category
Decomposition: The initial decomposition method. The following decomposition methods are currently supported: Sinclair, Pauli, Freeman-Durden, Generalized Freeman-Durden, Yamaguchi, van Zyl, Cloude and Touzi

Figure 5. Dialog box for the General Wishart classification

Reference:

[1] J.S. Lee and E. Pottier, Polarimetric Radar Imaging: From Basics to Applications, CRC Press, 2009

[2] J.S. Lee, M.R. Grunes, and E. Pottier, "Unsupervised terrain classification preserving polarimetric scattering characteristics", IEEE Transaction on Geoscience and Remote Sensing, Vol. 42, No. 4, April 2004.