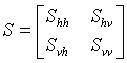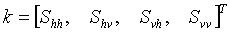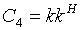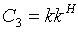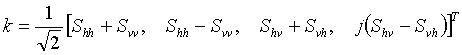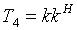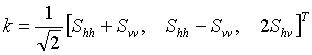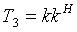Polarimetric Covariance or Coherency Matrices Generation
Operator
This operator creates the following polarimetric
covariance or coherency matrices for a given full polarimetric SAR
product:
- covariance matrix C3
- covariance matrix C4
- coherency matrix T3
- coherency matrix T4
Covariance Matrix C4
Let
be the complex Sinclair scatter matrix and
be the 4-D target vector, where
superscript T stands for the transpose operator. Then the
(4x4) covariance matrix C
4
is defined as
where superscript H represents the transpose
conjugate operator.
Covariance Matrix C3
For monostatic backscattering case, the transmitter
and the receiver are collocated. The reciprocity constrains the
Sinclair scattering matrix to be symmetrical, i.e. S
hv
= S
vh
. The 3-D target vector becomes
Then the (3x3) covariance matrix C
3
is given by
Cohrency Matrix T4
Let the 4-D target vector be defined as the
follows
Then the (4x4) coherency matrix T
4
is given by
Cohrency Matrix T3
For monostatic backscattering
case, the target vector becomes
Then the (3x3) coherency matrix T
3
is given by
Input and Output
- The input to this operator is a full polarimetric SAR product
with 8 bands, i.e. I and Q bands for HH, VV, HV and VH
polarizations.
- Since the output covariance or coherency matrix is Hermitian
positive semidefinite, only 9 elements in C3 or
T3 are independent, and 16 elements in
C4 or T4 are independent. Therefore only the
independent elements are output. For example, the following 9 bands
are output: C11, C22_real,
C12_imag, C13_real, C13_imag,
C22, C23_real, C23_imag,
C33 for covariance matrix C3.
Parameters Used
- Polarimetrix Matrix: The covariance or coherency
matrix type. The available types
are: C3, C4, T3 and
T4.
Reference:
[1] Jong-Sen Lee and Eric Pottier, Polarimetric Radar Imaging:
From Basics to Applications, CRC Press, 2009